Lab 4 - Podstawowe algorytmy przeszukiwania grafów - przeszukiwanie w głąb i wszerz


Metody i algorytmy planowania ruchu - laboratorium
Lab 4 - Podstawowe algorytmy przeszukiwania grafów - przeszukiwanie w głąb i wszerz

1. Wprowadzenie
Celem zajęć jest zapoznanie się z jedną z podstawowych struktur danych, która jest wykorzystywana do modelowania środowiska robota, grafem, oraz poznanie podstawowych algorytmów przeszukiwania grafów. Graf to struktura matematyczna służąca do modelowania relacji pomiędzy obiektami. Struktura ta składa się z obiektów, nazywanych w teorii grafów wierzchołkami oraz relacji pomiędzy tymi obiektami nazywanych krawędziami. Stąd graf definiuje się jako zbiór wierzchołków V oraz zbiór krawędzi E.
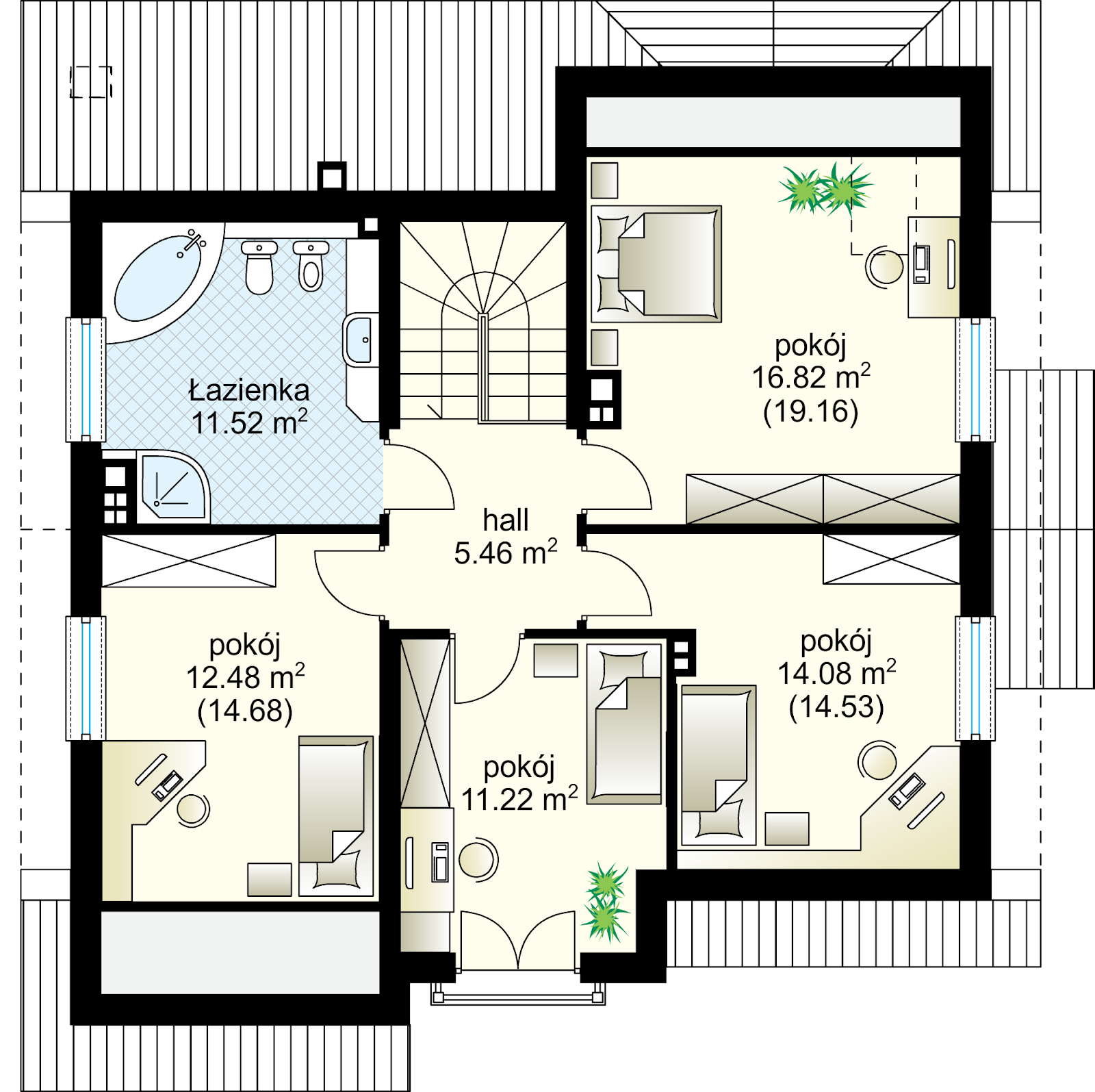
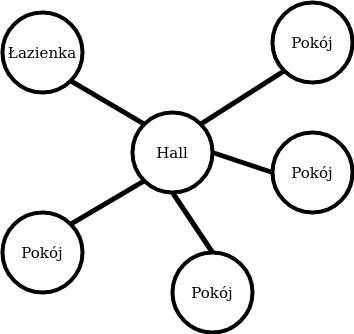
Grafy w kontekście planowania ruchu mogą reprezentować pewne lokacje i relacje pomiędzy nimi np. w przypadku przedstawionego na poniższym rysunku domu (po lewej), poszczególne pomieszczenia można traktować jako wierzchołki pewnego grafu (po prawej), natomiast krawędzie mogą reprezentować bezpośrednie przejście pomiędzy lokacjami. Reprezentacja otoczenia w postaci takiego grafu pozwala nam abstrahować od geometrii środowiska i jednocześnie skupić się na szerszej strukturze problemu przemieszczania się w tym środowisku tj. do którego pomieszczenia trzeba najpierw pojechać, aby przemieścić się pomiędzy pokojami.
 |
 |
|---|
Oczywiście powyższy przykład jest bardzo prosty, ale również bardziej złożone problemy wymagające planowania można zamodelować przy pomocy grafu.
Na poprzednich zajęciach zapoznawaliśmy się z mapami rastrowymi, mieliśmy do dyspozycji pewien uporządkowany zbiór, macierz komórek, które cechowały się np. prawdopodobieństwem zajętości (occupancy grid) czy wysokością (elevation map). To uporządkowanie w postaci macierzy daje się również przedstawić jako graf. W tym przypadku wierzchołkami są poszczególne komórki macierzy, a krawędziami przejścia pomiędzy sąsiadującymi komórkami. Zazwyczaj jako sąsiadujące komórki przyjmujemy te, które dzielą wspólną ścianę, a takie sąsiedztwo nazywamy czterosąsiedztwem (szare komórki są sąsiadami komórki z “x” w środku).
![]()
Wizualizację takiego grafu przedstawia poniższy rysunek:
![]()
Na czarno zaznaczono komórki macierzy mapy, natomiast na niebiesko i zielono, odpowiednio wierzchołki i krawędzie odpowiadającego jej grafu. Tego typu grafy będziemy przeszukiwać w dalszej części ćwiczenia. Poprzez przeszukiwanie rozumiemy procedurę systematycznego odwiedzania wierzchołków, począwszy od pewnego wyróżnionego wierzchołka startowego, i sprawdzania ich stanu np. czy dany wierzchołek jest poszukiwanym celem.
⚠️ Pamiętaj, aby w każdym nowym terminalu zanim rozpoczniesz pracę skonfigurować środowisko ROS komendą
source /opt/ros/humble/setup.bashlubsource install/setup.bash
2. Przygotowanie paczki w ROS
Zainstaluj paczkę ros-humble-nav2-map-server:
sudo apt-get install ros-humble-nav2-map-server ros-humble-nav2-lifecycle-managerPobierz paczkę z zadaniami z repozytorium github:
cd ~/ros2_ws/src
git clone https://github.com/BartlomiejKulecki/mapr_4_student.gitNastępnie skompiluj pobraną paczkę i odśwież przestrzeń roboczą:
cd ~/ros2_ws
colcon build --symlink-install
source install/setup.bashZapoznaj się z udostępnionym kodem. W szczególności z plikiem
points.py, w którym znajduje się definicja
węzła publikującego punkt początkowy i końcowy oraz z plikiem
grid_map.py definiującym klasę
GridMap, z której dziedziczyć będzie klasa, w której
zaimplementujesz algorytmy przeszukiwania.
3. Przeszukiwanie w głąb (Depth First Search - DFS)
Algorytm przeszukiwania należy zaimplementować w pliku dfs.py w polu oznaczonym komentarzami (zawierają one przydatne informacje dotyczące dostępnych metod).
🔨 Zadanie 3.1
Wypełnij metodę search klasy DFS tak, aby
realizowała algorytm przeszukiwania w głąb, biorąc pod uwagę, że
niektóre komórki są zajęte (wartość komórki ustawiona na 100 -
reprezentują przeszkody, których nie należy odwiedzać), publikując co
krok mapę zajętości (odwiedzone komórki oznaczaj wartością 50) i
wyświetlając w konsoli informację o znalezieniu wierzchołka końcowego po
jego odwiedzeniu.
Kod uruchamia się poleceniem:
ros2 launch mapr_4_student dfs_launch.pySpodziewany efekt (szybkość aktualizacji mapy zależy od argumentu
delay metody publish_visited):
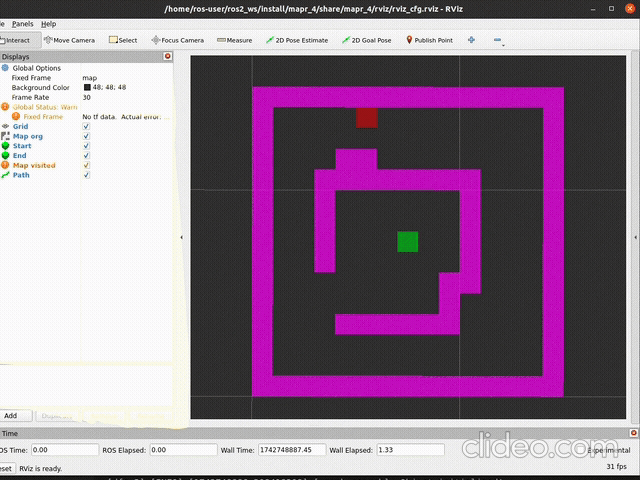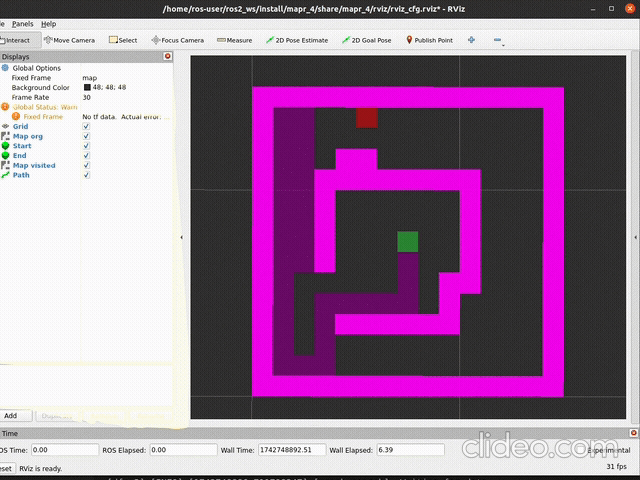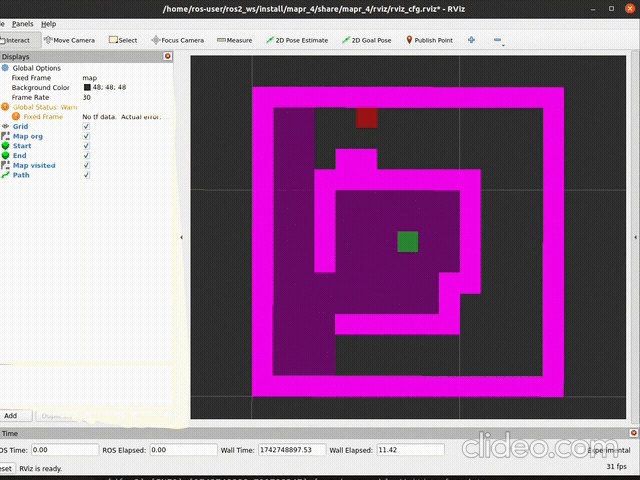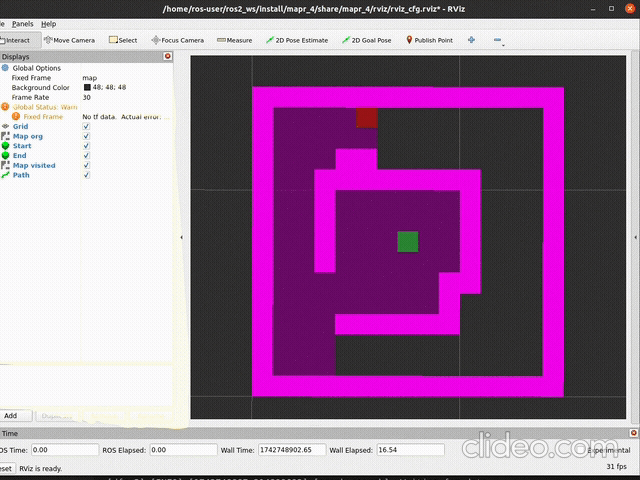 |
 |
|---|---|
| działanie | stan końcowy |
Wskazówka 1 - przykładowe działanie
Algorytm powinien odwiedzić wierzchołki w następującej kolejności, przy założeniu że wierzchołek oznaczony numerem “0” był początkowym wierzchołkiem oraz że kolejność sprawdzania sąsiadów jest dana poniższym schematem. Zaznaczony został układ współrzędnych związany z mapą.
![]()
Wskazówka 2 - pseudokod
I. Dodaj wierzchołek początkowy do listy (stosu) wierzchołków do odwiedzenia
II. Dopóki lista (stos) wierzchołków do odwiedzenia nie jest pusta:
A. Odczytaj pierwszy wierzchołek ze stosu i zaznacz go jako odwiedzony
B. Sprawdź, czy ten wierzchołek jest poszukiwanym wierzchołkiem końcowym
1. Jeśli tak: zakończ algorytm
2. Jeśli nie, to sprawdź czy ten wierzchołek ma sąsiada, który nie jest odwiedzony i nie jest zajęty (nie jest ścianą)
a) Jeśli tak, to dodaj tego sąsiada do stosu i idź do pkt. II.
b) Jeśli nie, to usuń bieżący wierzchołek ze stosu i idź do pkt. II.🔨 Zadanie 3.2
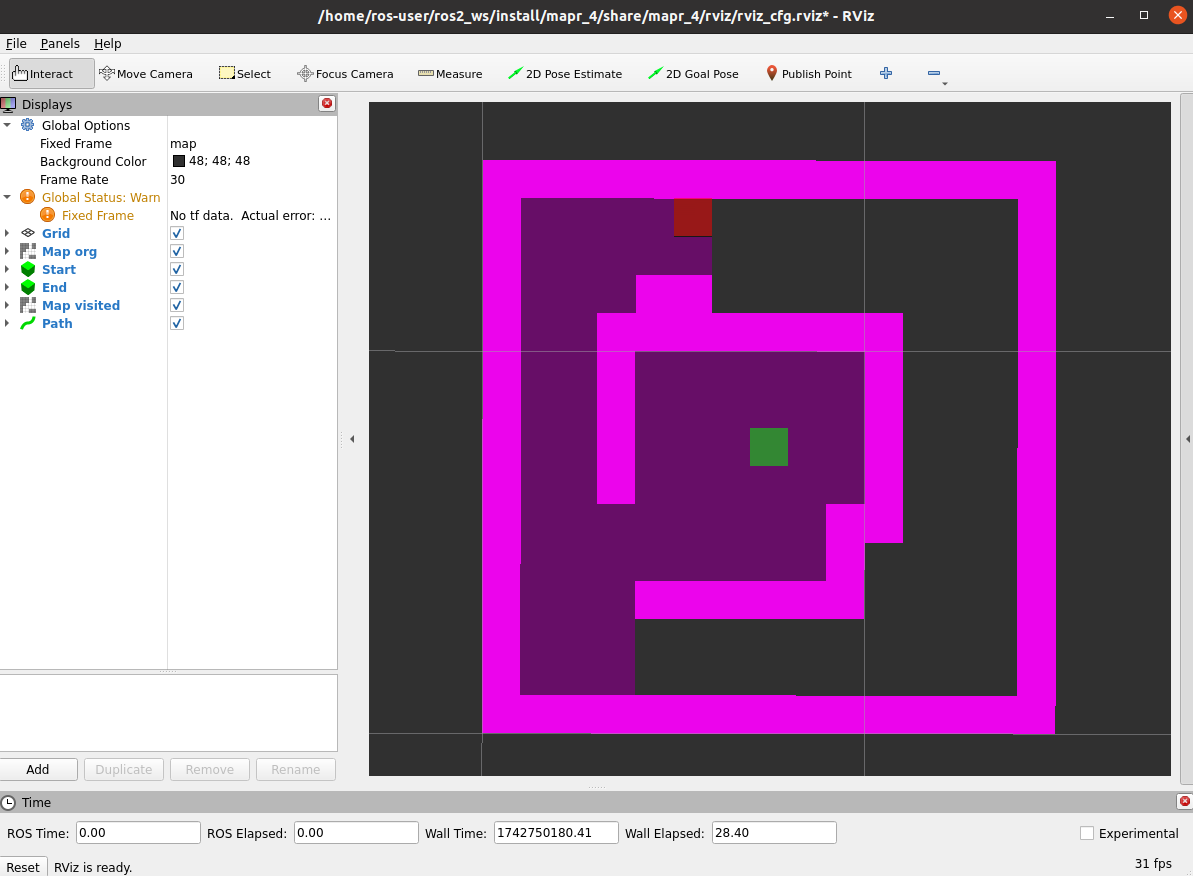
Wyznacz ścieżkę łączącą początkowy wierzchołek z wierzchołkiem celu
odkrytą przez algorytm (lista tupli z indeksami poszczególnych komórek -
dane zapisane na stosie). Na koniec działania algorytmu wyświetl tę
ścieżkę, korzystając z metody publish_path. Kod zapisz w
pliku dfs_backtrace.py (skopiuj kod z pliku
dfs.py), do wyświetlenia rezultatów użyj
polecenia:
ros2 launch mapr_4_student dfs_launch.py backtrace:=True Spodziewany efekt:
![]()
4. Przeszukiwanie wszerz (Breadth First Search - BFS)
Algorytm przeszukiwania należy zaimplementować w pliku bfs.py w polu oznaczonym komentarzami (zawierają one przydatne informacje dotyczące dostępnych metod).
🔨 Zadanie 4.1
Wypełnij metodę search klasy BFS tak, aby
realizowała algorytm przeszukiwania wszerz, biorąc pod uwagę, że
niektóre komórki są zajęte (wartość komórki ustawiona na 100 -
reprezentują przeszkody, których nie należy odwiedzać), publikując co
krok mapę zajętości (odwiedzone komórki oznaczaj wartością 50) i
wyświetlając w konsoli informację o znalezieniu wierzchołka końcowego po
jego odwiedzeniu.
Kod uruchamia się poleceniem:
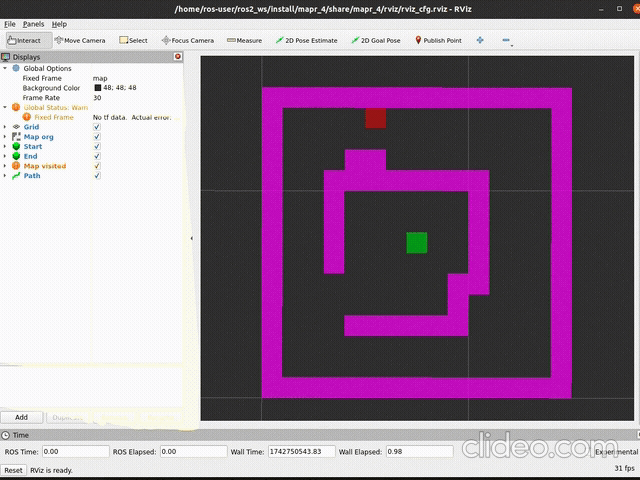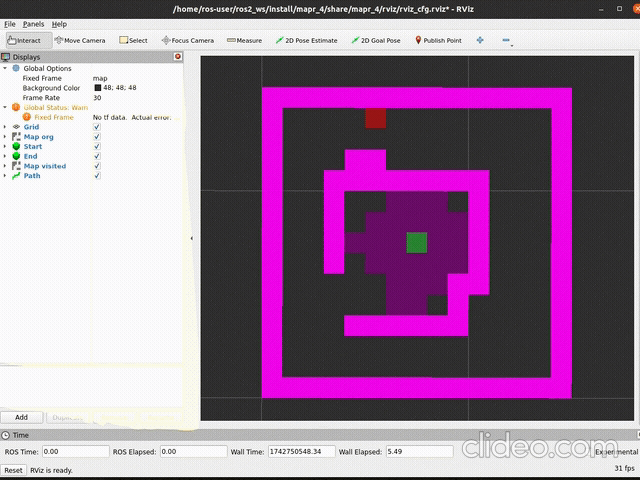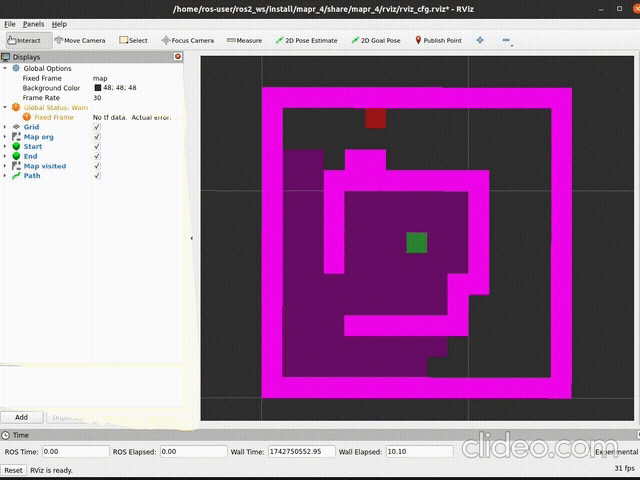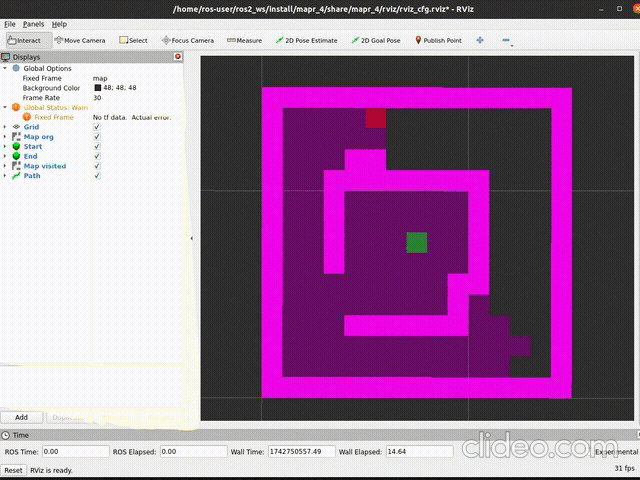
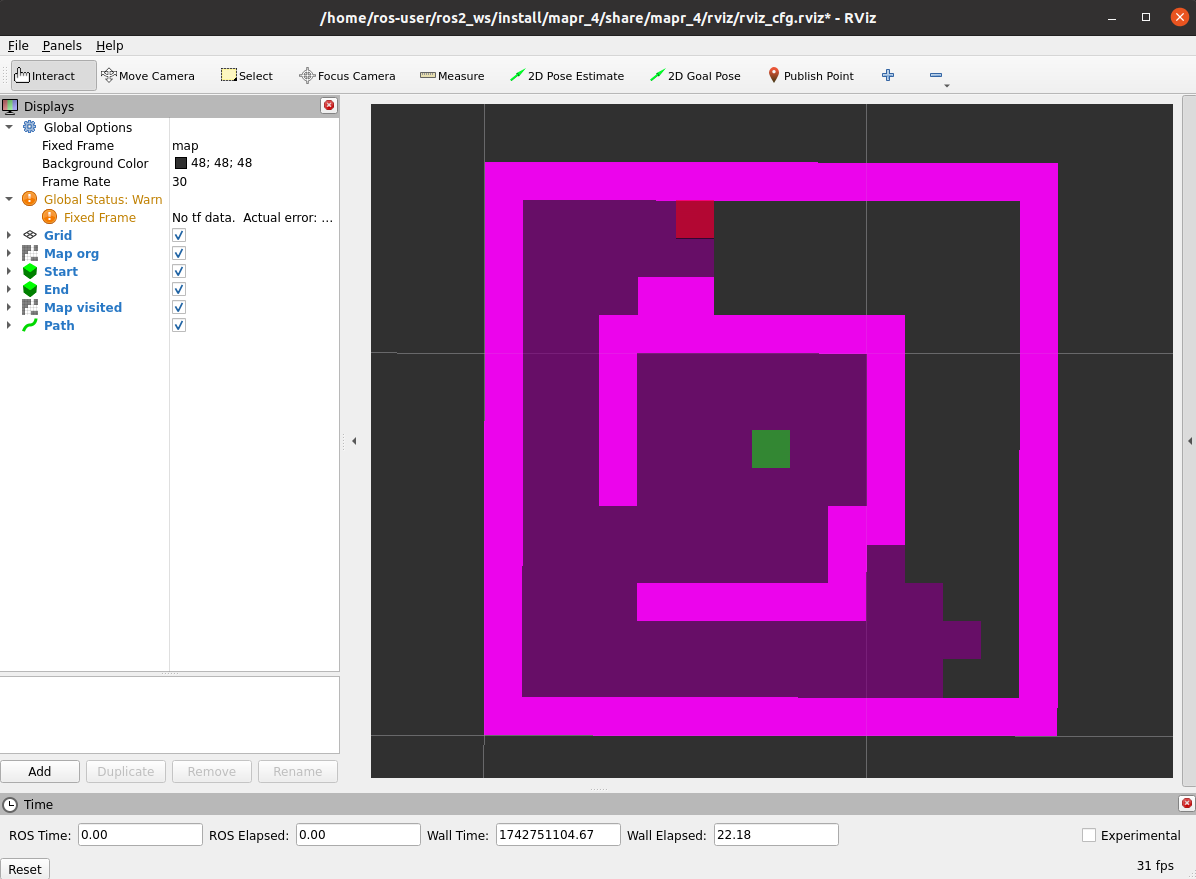
ros2 launch mapr_4_student bfs_launch.pySpodziewany efekt (szybkość aktualizacji mapy zależy od argumentu
delay metody publish_visited):
 |
 |
|---|---|
| działanie | stan końcowy |
Wskazówka 1 - przykładowe działanie
Algorytm powinien odwiedzić wierzchołki w następującej kolejności, przy założeniu że wierzchołek oznaczony numerem “0” był początkowym wierzchołkiem oraz że kolejność sprawdzania sąsiadów jest dana poniższym schematem. Zaznaczony został układ współrzędnych związany z mapą.
![]()
Wskazówka 2 - pseudokod
I. Dodaj wierzchołek początkowy do listy (kolejki) wierzchołków do odwiedzenia
II. Dopóki lista (kolejka) wierzchołków do odwiedzenia nie jest pusta:
A. Odczytaj pierwszy wierzchołek z kolejki i zaznacz go jako odwiedzony
B. Sprawdź, czy ten wierzchołek jest poszukiwanym wierzchołkiem końcowym
1. Jeśli tak: zakończ algorytm
2. Jeśli nie, to:
a) Dodaj do kolejki każdego sąsiada, który nie jest odwiedzony (i którego nie ma jeszcze w kolejce) i nie jest zajęty (nie jest ścianą)
b) Usuń bieżący wierzchołek z kolejki, idź do pkt. II.🔨 Zadanie 4.2.
Wyznacz ścieżkę łączącą początkowy wierzchołek z wierzchołkiem celu
odkrytą przez algorytm (lista tupli z indeksami poszczególnych komórek).
W tym celu warto dla każdego węzła zapisywać indeksy węzła
poprzedzającego w grafie i aby znaleźć ścieżkę, przejść po indeksach od
punktu końcowego do początkowego. Na koniec działania algorytmu wyświetl
tę ścieżkę, korzystając z metody publish_path. Kod zapisz w
pliku bfs_backtrace.py (skopiuj kod z pliku
bfs.py), do wyświetlenia rezultatów użyj
polecenia:
ros2 launch mapr_4_student bfs_launch.py backtrace:=True Spodziewany efekt:
![]()